보드게임을 위한 인공지능 알고리즘
- 오목(Gomoku)은 한 쪽의 이익이 다른 한쪽의 손실을 의미하는 제로섬(Zero-Sum) 게임이다.
- 제로섬 게임에 활용되는 Minimax 알고리즘과 Alpha-Pruning 알고리즘의 동작 원리를 이해할 수 있다.
제로섬 알고리즘의 원리
- Minimax 알고리즘은 인공지능과 사람이 모두 최적에 가까운 수를 둔다는 가정을 두고 논리를 전개한다.
- 어떠한 상황이 최적인 지를 구분해주는 역할을 수행하는 인공지능 내부의 평가 함수의 성능이 중요하다.
평가함수
- 평가 함수의 효율성이 높을 수록 강력한 인공지능이 탄생할 수 있다.
- 따라서 인공지능 개발자의 입장에서 오목 게임의 특징에 대해서 바르게 이해할 필요가 있다.
아래에서 ‘오목’, ‘열린 사’, ‘열림 삼’, ‘닫힌 삼’ 등을 고려하여 인공지능 알고리즘에 적용하는 방식의 평가함수를 사용
Minimax 알고리즘
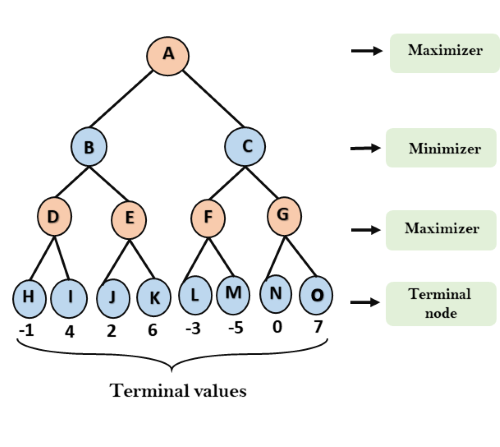
- 2인 제로섬 게임(Zero_sum Game)에서 가장 기본이 되는 알고리즘 중 하나
- Minimax 알고리즘은 정해진 Depth까지 노드의 가짓수를 탐색하는 알고리즘이다.
- Minimax는 모든 플레이어가 합리적으로 가정을 하므로, 우리는 우리의 상황에 대한 평가가 높은 경우 만을
선택하고, 상대방은 우리의 상황에 대한 평가가 낮은 경우만을 선택한다고 가정한다.
- 이러한 원리를 압축하여 우리를 Max, 상대방을 Min으로 정한다.
깊이 우선 탐색(DFS 방식을 사용)
전수조사를 해야한다는 점에서 비효율적이다.

Alpha-Beta Pruning 알고리즘
- Minimax 알고리즘 기반으로 효율성을 개선한 알고리즘
- 도달할 가능성이 없는 노드들은 탐색하지 않도록 가지를 친다
ex) Max 노드의 Min 자식 노드 중 하나가 3이라는 값을 가진다면, Max 노드가 가지게 될 값은 항상 3이상이다.
이때부터는 Max의 Min 자식 노드 중에서 그 자식 Max 노드가 3 이핫의 값을 가지는 노드가 하나라도 존재
한다면 해당 Min 노드는 더 이상 탐색하지 않아도 된다.
평가함수의 작성
- Minimax 알고리즘 및 Alpha-Beta Pruning 알고리즘은 이미 정해진 작성 방법이 존재한다.
- 하지만 평가 함수는 완벽한 해법이 정해져 있지 않으므로, 알고리즘 설계자가 임의로 설정할 수 있다.
- 평가 함수 알고리즘의 효율성 개선에 초점을 맞춘 연구가 필요하다.
오목 게임에서의 평가 함수
- 열린 사가 닫힌 삼보다 강력한 수라는 것은 실험적으로 증명할 필요 없이 당연하다.
- 하지만 열린 삼의 가치가 닫힌 사보다 가치로운지 등의 내용에 대해서는 깊게 고민할 필요가 있다.
- 특정 상황에 대한 가치 평가를 정량화 할 필요가 있다.
특정한 돌의 패턴에 대한 가치 산정
1) 열린 오: 100,000
2) 열린 사: 20,000
3) 하나 닫힌 사: 5,000
4) 열린 삼: 4,000
5) 닫힌 사: 1,500
6) 하나 닫힌 삼: 1,500
7) 열린 이: 1,500
8) 닫힌 삼: 300
9) 하나 닫힌 이: 300
10) 닫힌 이: 50
바둑판의 천원점과 가까울 수록 점수 가산